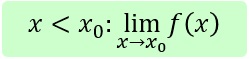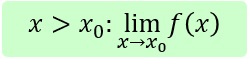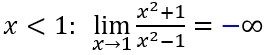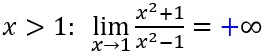Eine Polstelle (auch senkrechte Asymptote genannt), nennen wir sie x₀, ist dadurch gekennzeichnet,
dass, wenn man sich von links oder rechts der Stelle x₀ annähert, die Funktionswerte gegen plus oder minus unendlich gehen.

Polstellen können an den Nullstellen des Nenners auftreten, müssen aber nicht!

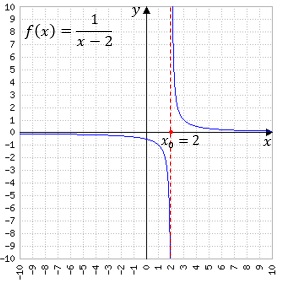
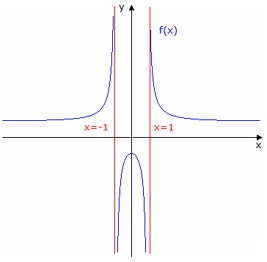
In der nebenstehenden Abbildung hat f(x) bei x₀ eine Polstelle, wenn x₀ eine Nullstelle des Nenners ist und der Zähler nicht gleichzeitig 0 oder ∞ wird.

Es gibt Polstellen mit bzw. ohne Vorzeichenwechsel (VZW).

In der Abbildung sehen wir eine Polstelle mit Vorzeichenwechsel, da beim "Überschreiten" der Polstelle von links nach rechts das Vorzeichen von - nach + wechselt.

Lücken statt Polstellen

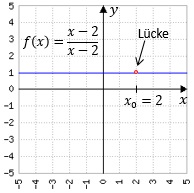
Der "pathologische" Fall tritt dann ein, wenn bei x₀ eine Nullstelle des Nenners vorliegt aber auch der Zähler Null wird. Die Funktion 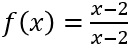hat bei x₀=2 eine Nullstelle des Nenners, aber auch des Zählers. Damit wäre f(2)=0/0, aber dies ist nicht definiert! f(x) hat bei x₀=2 eine Definitionslücke aber keine Polstelle!

Beachte
Schließe diejenigen x₀ aus den Kandidaten für Polstellen aus, bei denen der Zähler 0 oder ∞ wird!

Konstruktion von Funktionen mit Polstellen

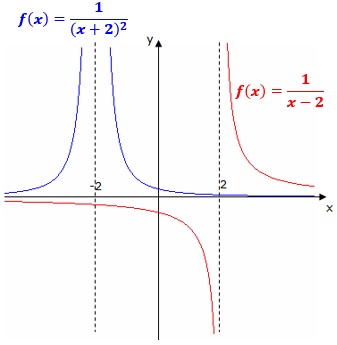
Wenn f(x) bei x=a eine Polstelle haben soll, so brauchen Sie einen Nenner der Form .

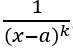Für gerade k ergibt sich eine Polstelle ohne Vorzeichenwechsel, ungerade k liefern eine Polstelle mit Vorzeichenwechsel.






Vorzeichenuntersuchung

Annäherung von links:

Annäherung von rechts:

Die obigen Formeln bedeuten, dass man das Vorzeichen links und rechts der Polstelle dadurch feststellt, dass man einen etwas kleineren und einen etwas größeren x-Wert als x₀ einsetzt. Man kann dies natürlich im Kopf durchdenken, aber bei komplizierteren Funktionstermen ist es ratsamer, den GTR zu verwenden, sofern es sich um eine Wahlteil-Aufgabe handelt.

Rechenbeispiel

Untersuche 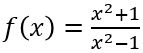auf Polstellen.

Lösung

Die Nullstellen des Nenners sind x₀=1 und x₁=-1
In beiden Fällen wird der Zähler nicht 0 oder ∞, somit handelt es sich tatsächlich um Polstellen!






Vorzeichenuntersuchung der Polstelle bei x₀=1

Annäherung von links:	für x "nahe" 1 und x<1 (z.B. x=0,9) wird der Nenner negativ!
Annäherung von rechts:	für x "nahe" 1 und x>1 (z.B. x=1,1) sind Zähler und Nenner positiv!

Ergebnis: Bei x₀=1 liegt eine Polstelle mit Vorzeichenwechsel (von - nach +) vor.
Analog liegt bei x₁=-1 eine Polstelle mit Vorzeichenwechsel (von + nach -) vor.


Wahlteil 2009 Analysis I 1 a)
(Wiedergegeben wird nur ein Auszug aus der Aufgabenstellung, nämlich der Teil, der für unser Thema relevant ist.)

Gegeben ist eine Funktion f mit .

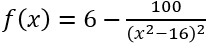Geben Sie sämtliche Asymptoten des Schaubilds von f an.
Skizzieren Sie das Schaubild von f samt Asymptoten für -7≤x≤7.

Asymptoten
Wegen 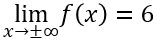ist die Gerade y=6 eine waagrechte Asymptote von f.

Polstellen
Die Nullstellen des Nenners sind die Polstellen von f. (Beachte: An diesen Stellen wird der Zähler nicht gleichzeitig 0!) Die Nullstellen des Nenners sind: x₁=-4 und x₂=4.

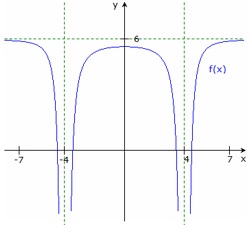
In die nachfolgende Skizze können wir also bei y=6 eine waagrechte Gerade und bei x=-4 sowie bei x=4 senkrechte Geraden einzeichnen. Vorzeichenuntersuchungen an den Polstellen benötigen wir nicht, da es sich um eine Wahlteilaufgabe handelt und wir den Kurvenverlauf mit dem GTR zeichnen lassen können.

Skizze